October 2024
The Grubbs’ Test for outliers is one of the new techniques in the just release SPC for Excel version 7. To view what is new in version 7, please select this link. To see all the statistical tools in SPC for Excel, please select this link.

What happens to your calculations if there are outliers present in the data? They could easily become skewed because of the outliers, and you could draw the wrong conclusions. There are several ways to detect outliers in a data set. One method is called the Grubbs’ test. This test is introduced in this publication.
In this publication:
- Introduction
- Example Data
- Grubbs’ Test Calculations: Two-Sided
- Visual Conformation
- Grubbs’ Test Calculations: One-Sided
- Summary
- Quick Links
Please feel free to leave a comment at the end of the publication. You can download a pdf copy of this publication at this link.
Introduction
The Grubbs’ test is a hypothesis test. The null (H0) hypothesis and alternate (H1) hypothesis are given below.
H0: The sample results are all from the same population
H1: One of the sample results are not from the same population
Note that the alternate hypothesis is that just one sample is not from the same population. To perform the Grubbs’ test, it is assumed that the data comes from a normal distribution. You can create a normal probability plot and calculate the Anderson-Darling statistic to confirm that your data are normal. For more information on this, please see our SPC Knowledge Base article The Anderson-Darling Test for Normality.
The Grubbs’ test is fairly straight forward. You collect your random samples and measure each sample. You should always look at your data to see if any data point looks like it is a potential outlier. If you have any doubts, you need to check to see if the point is an outlier.
If you are using the Grubbs’ test you will be calculating a “G” test statistic. Yes “G” for Grubbs. But before you do that calculation, you must decide on which of three cases you want to test:
- Test whether the smallest value is an outlier
- Test whether the largest value is an outlier
- Test the two sided case (either smallest or largest value) for the outlier
The formula for G is different depending on which test you select.
The other thing you must decide on is the value of alpha. Alpha (a) is called the significance level. Typical values of alpha are 0.05 and 0.10. The significance level gives the risk of concluding that an outlier exists when there is no outlier. So, a value of 0.05 for alpha means that is a 5% risk of concluding that an outlier exists when one does not exist.
You will be calculating a p-value. The p-value is the probability of obtaining the calculated G test statistic if the null hypothesis is true. If the p-value is small (less than the alpha you selected), then you conclude that the probability of getting the calculated G test statistic is small and you reject the null hypothesis. If the p-value is large (greater than the alpha value you selected), you then conclude that the probability of getting the calculated G test statistic is large. You accept the null hypothesis and conclude that there are no outliers.
Let’s see how this works with some actual data.
Example Data
Suppose you have collected 30 samples and measured each sample for a quality characteristic, X. The data are shown in Table 1.
Table 1: Example Data
|
Sample |
X |
Sample |
X |
|
|
1 |
97.1 |
16 |
91.7 |
|
|
2 |
94.8 |
17 |
110.2 |
|
|
3 |
86.0 |
18 |
90.9 |
|
|
4 |
99.4 |
19 |
113.4 |
|
|
5 |
94.5 |
20 |
122.9 |
|
|
6 |
87.9 |
21 |
99.7 |
|
|
7 |
96.9 |
22 |
93.5 |
|
|
8 |
102.0 |
23 |
91.9 |
|
|
9 |
93.2 |
24 |
86.7 |
|
|
10 |
93.0 |
25 |
98.6 |
|
|
11 |
147.9 |
26 |
97.1 |
|
|
12 |
106.2 |
27 |
109.3 |
|
|
13 |
93.4 |
28 |
93.1 |
|
|
14 |
104.8 |
29 |
105.8 |
|
|
15 |
114.6 |
30 |
109.6 |
We will use this data to demonstrate how the Grubbs’ test works.
Grubbs’ Test Calculations: Two-Sided
The first step is to decide on the Grubb’s test that we will use. We will use the two-sided test so the outlier can be either the maximum value or minimum value in the data set. The second step is to select alpha. We will use 0.05 in this example. The equation for the two-side G test statistic is given by:
where y is the sample average, s is the sample deviation, ymin is the minimum value, and ymax is the maximum value.
You can perform the basic calculations for the data in Table 1:
y = 100.87
s = 12.62
ymin = 86.0
ymax = 147.9
The G test statistic can then be calculated:
What is the G test statistic measuring for the two sided test? It is comparing the number of standard deviations the minimum value is from the average to the number of standard deviations the maximum value is from the average. The G test statistic is the larger of those two – the one most likely to be an outlier.
In this example, the maximum is 3.73 standard deviations from the average.
Now, we must address the question of how likely we are to get a value of 3.73 if there are no outliers. A p-value needs to be calculated. The calculations for the p-value for the two-sided G test statistic are given below.
where N is the number of values (30 in our example), and P is the probability of T being greater than the terms under the square root. T has N-2 degrees of freedom.
p-value = 2(30)P(T > 5.25)
To calculate the probability that T is greater than 5.25, you can use the TDIST function in Excel.
P(T > 5.25)= TDIST(5.25, 28, 1) = 0.000007
This gives a p-value:
p-value = 2(30)(0.000007 ) = 0.0004
Since the p-value is small, we conclude that the probability of getting a G test statistic equal to 3.73 is very small, and there is an outlier present. The maximum value is an outlier.
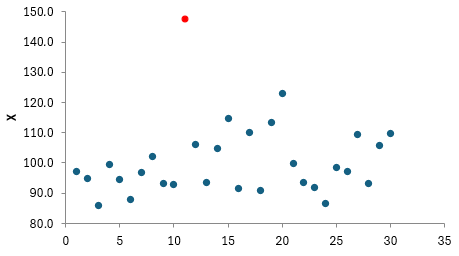
Visual Confirmation
You can confirm that the maximum value is an outlier by plotting the points on a run chart as shown in Figure 1.
Figure 1: Run Chart
It is easy to see that the maximum point lies well beyond the other data. You will usually plot the data first and then use the Grubbs’ test to confirm that an outlier exists.
Grubbs’ Test Calculations – One Sided
The example above was the two-sided Grubbs test – looking at both minimum and the maximum. You can also do one-sided tests if you are sure that the outlier may be a minimum or may be the maximum. The equations for these tests are given below.
Test whether the smallest value is an outlier
The G test statistic for testing if the minimum value is an outlier is given below:
G = (y – ymin)/s
The p-value is given by:
Test whether the largest value is an outlier
The G test statistic for testing if the largest value is an outlier is given by:
G = (ymax – y )/s
The p-value is given by the same equation for testing if the minimum value is the outlier.
Summary
This publication has introduced Grubbs’ test for an outlier. The data must be normally distributed. The G test statistic is calculated for either the one-sided or two-sided test. The value of alpha is set so that it can be compared to the p-value. If the p-value is less than alpha, then you reject the null hypothesis and assume that there is an outlier present. If the p-value is greater than alpha, then you accept the null hypothesis and assume there are no outliers present. This test only determines if there is one outlier.
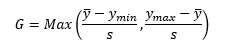
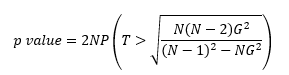
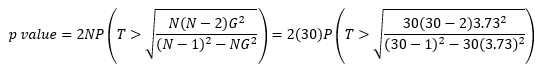
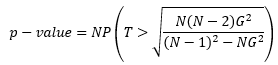
Wow, thanks for the memory. We used this on my BSc Applied Statistics course at Sheffield back in 1974-1978. Happy timees.